On a finite time scale
It was rumored that updates to the MacBook Pro were coming at WWDC. These rumors did not pan out. Instead it looks like the new MacBook Pro will be landing sometime later this year, possibly due to delays in availability of high end Skylake 45w mobile parts. This seems plausible, given that Intel only released its Skylake quad core NUC in mid-May. The magnitude of these delays has certainly made its way around the tech press, but are these delays really exceptional?
This quick exploratory analysis of the significance of these delays was performed using historical delays between iterations. The source of this release dates was from the Wikipedia pages for each of these products. A csv file including this data has been made available here. For the retina and non-retina release dates are given for only the retina versions of products once they become available.
Notably absent from this analysis is the MacBook Air and MacBook. In the former case the dates were not present on the Wikipedia article, and in the later case there wasn't sufficient data to do anything but interpolate.
Overview
For this exploratory analysis two models were used. The first model, linear regression with one predictor (see Figure 1.), assumes that there is a constant interval between releases over time. Deviations from this release cycle are just model error. The second model is a differenced regression model. In this linear model, release dates are replaced with differences between release dates. This allows for a trend in the release dates, such as increasing delays between releases.
This analysis treats future releases and delays as a prediction problem. Therefore, prediction intervals are used to determine significance. The level of significance is set to 5% for the two sided interval, however our interest is really at large delays giving us a one-sided confidence level of to 2.5% for our analysis. Inference including point estimates and prediction intervals are based on standard ordinary least squares (OLS) assumptions. In both models, time is treated as the dependent variable with product iteration as the independent variable. Time is represented as days since epoch, where epoch is set at 0 equal to January 1, 1970.
This problem is actually a wait-time problem, so normality is used as an approximation to modeling with gamma distributed errors or other slightly more difficult approaches. Still, the regression approach seems to be 'good enough' for this blog post. In the future I'll revisit more complex models.
macRelease <- read.csv('macrelease.csv') macRelease$releaseDate <- as.Date( macRelease$Release.date, format="%d %B %Y") library(ggplot2) theme_set(theme_gray(base_size = 20)) # plot product release dates by iteration p <- ggplot(macRelease, aes(x=Iteration, y=releaseDate, group=Product)) p + geom_line(aes(color=Product),size=1) + geom_point(aes(color=Product),size=3) + labs( title='Apple Product Iteration by Release Date', y="Release Date")
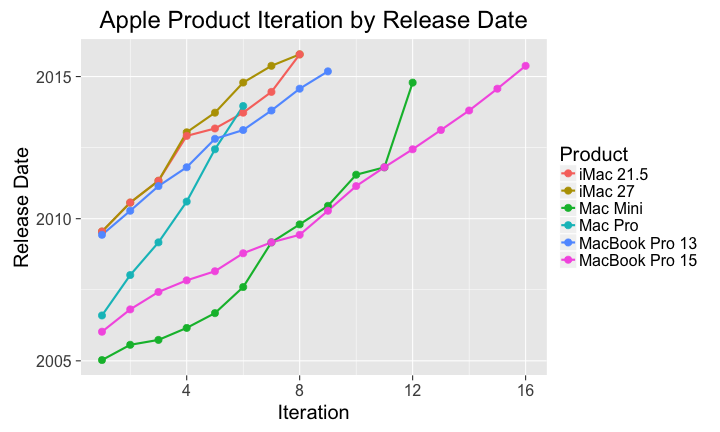
The significance of the results differ considerably by model. According to the first model used, all but the 27" iMac are past the expected release date. Of these delayed products, all but the 21.5" iMac, has a significant delay.
# linear model by product library(dplyr) #get unique factors as string currentProducts <- unique(macRelease$Product) # create a place to save our predictions releaseInterval <- c() # get a specific product for( i in 1:length(currentProducts)) { currentProduct <- filter(macRelease,Product==currentProducts[i]) # produce a product scatterplot with a linear model overlay p <- ggplot(currentProduct, aes(x=Iteration, y=releaseDate)) + geom_point() p <- p + geom_smooth(method ="lm",se=TRUE) + labs( title=currentProducts[i], x="Iteration", y="Release Date") plot(p) # converting time to something linear we do our prediction fit <- lm( as.numeric(releaseDate) ~ Iteration, data=currentProduct) pred <- predict( fit, data.frame( Iteration=nrow(currentProduct)+1), interval="prediction") releaseInterval <- rbind( releaseInterval, pred) }
rownames(releaseInterval) <- currentProducts # using epoch we get a date range conversion start.date <- as.Date("1970-01-01") releaseInterval <- as.data.frame(releaseInterval) releaseInterval$fit <- as.character(as.Date(releaseInterval$fit,origin=start.date)) releaseInterval$lwr <- as.character(as.Date(releaseInterval$lwr,origin=start.date)) releaseInterval$upr <- as.character(as.Date(releaseInterval$upr,origin=start.date))
| Product | Expected Release Date | Lower Bound | Upper Bound |
|---|---|---|---|
| iMac 27 | 2017-03-28 | 2016-02-02 | 2018-05-22 |
| iMac 21.5 | 2016-06-19 | 2015-06-13 | 2017-06-27 |
| Mac Mini | 2014-01-26 | 2012-03-02 | 2015-12-22 |
| Mac Pro | 2015-04-15 | 2014-06-20 | 2016-02-08 |
| MacBook Pro 13 | 2016-01-02 | 2015-07-08 | 2016-06-29 |
| MacBook Pro 15 | 2015-07-11 | 2014-10-10 | 2016-04-09 |
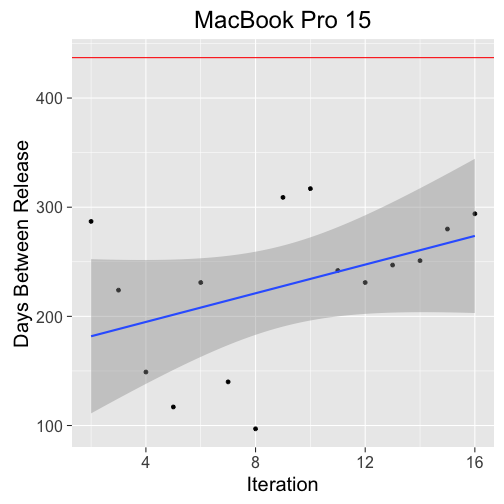
The second model is a bit more accepting of delays. The MacBook Pros and the Mac Pro have significant delays, marginally so for the Mac Pro. The significance of the 15" MacBook Pro is in part to it's highly regular release schedule. The negative values in the lower bound indicate that the normality assumption may be problematic.
| Product | Expected Delay (Days) | Lower Bound | Upper Bound | Delay as of 29 July, 2016 |
|---|---|---|---|---|
| iMac 27 | 213.61 | -242.05 | 669.27 | 290.00 |
| iMac 21.5 | 317.64 | -244.61 | 879.90 | 290.00 |
| Mac Mini | 565.73 | -101.98 | 1233.44 | 653.00 |
| Mac Pro | 603.40 | 257.63 | 949.17 | 953.00 |
| MacBook Pro 13 | 220.33 | 0.09 | 440.57 | 508.00 |
| MacBook Pro 15 | 273.71 | 113.57 | 433.85 | 437.00 |
In both models the delay before the release of the latest Mac Mini is a fairly significant outlier. This increase in delay may indicate a change in update frequency. If this is a change in frequency, then inference using the first model with OLS assumptions is inappropriate due to the error term not being identically distributed. The presence of a good covariate may fix this issue, but it is unknown what covariate would describe this delay. The difference model may also be inappropriate under this change due the presence of heteroscedasticity.
diffInterval <- c() #get a specific product for( i in 1:length(currentProducts)) { currentProduct <- filter(macRelease,Product==currentProducts[i]) # get differences refreshDiff <- cbind( diff(currentProduct$releaseDate), 2:nrow(currentProduct) ) # add on some column names and make a data frame colnames(refreshDiff) <- c('Days','Iteration') refreshDiff <- as.data.frame(refreshDiff) # converting time to something linear we do our prediction fit <- lm( as.numeric(Days) ~ Iteration, data=refreshDiff) pred <- predict( fit, data.frame( Iteration=nrow(refreshDiff)+1), interval="prediction") # get the difference between the last date, and today's date todayDiff <- as.numeric(Sys.Date() - last(currentProduct$releaseDate) ) diffInterval <- rbind( diffInterval, c(pred,todayDiff)) # plot the times betweeen iteration p <- ggplot(refreshDiff, aes(x=Iteration, y=as.numeric(Days))) + geom_point() p <- p + geom_smooth(method="lm") + labs( title=currentProducts[i], x="Iteration", y="Days Between Release") + geom_hline(yintercept=todayDiff, col='red') plot(p) }
rownames(diffInterval) <- currentProducts
Product Release Dates
iMac 27"
Expected Update: 2017-03-28 with 95% prediction interval (2016-02-02, 2018-05-22).
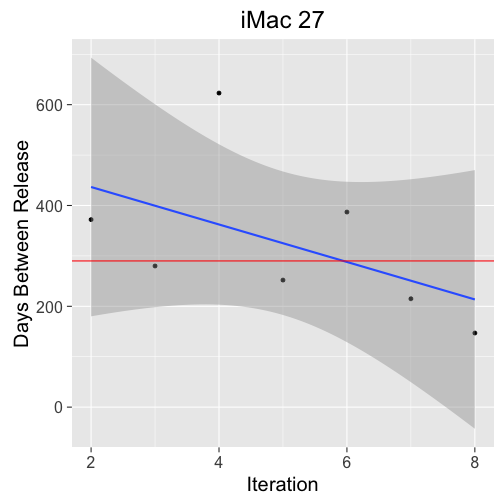
Looking at the 27" iMac we can see that it is frequently updated. The substance of the updates may be in question, but it certainly is at least getting some love.
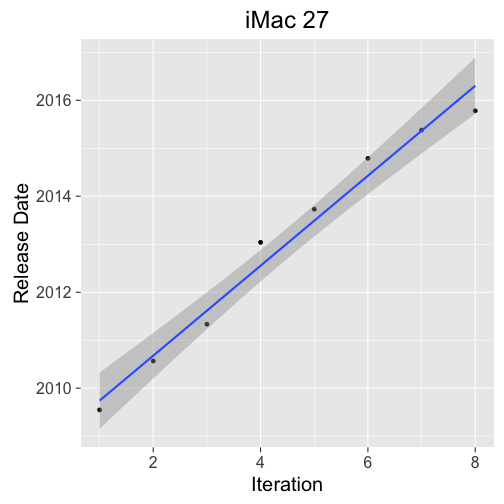
Furthermore, we can see a decrease in time between updates, and the 27" iMac is the only current product to get the Skylake treatment. The number of iterations and variability in release dates make this analysis problematic, so the prediction interval takes us way out to mid 2018.
iMac 21.5"
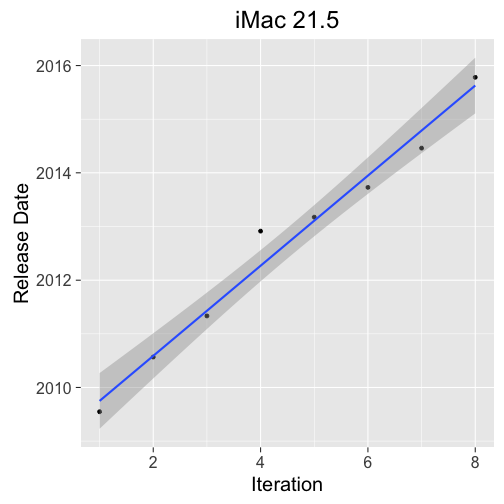
Expected Update: 2016-06-19 with 95% prediction interval (2015-06-13, 2017-06-27).
The 21.5" iMac is a bit of an oddity; it is still using Broadwell, possibly due to its reliance on integrated graphics. Despite the slightly older CPU architecture, relative to it's big sister, this mac is still being regularly updated. As some degree of evidence that someone at Apple cares about this product, it did make its way into the Retina-age last update.
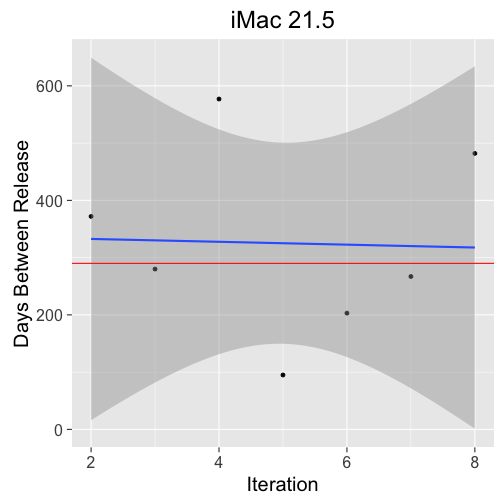
As before with the 27" iMac, the data is a bit of a mess. Looking at the plot of iterations verse days between releases, the slope has a fair bit of play leading to the fairly wide prediction interval.
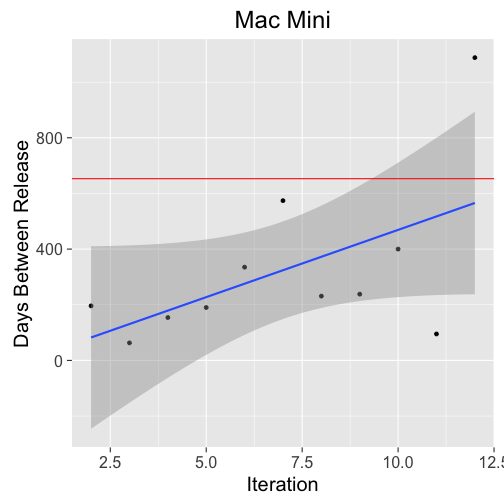
Mac Mini
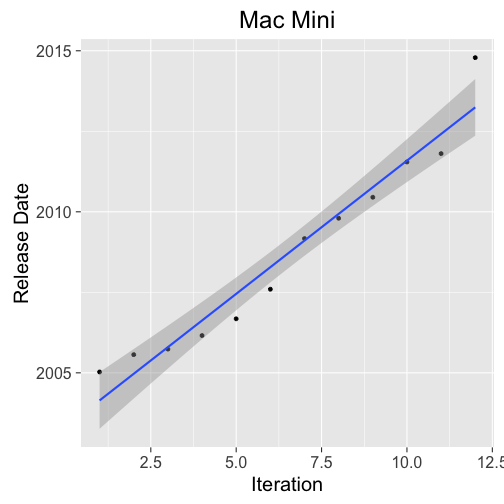
Expected Update: 2014-01-26 with 95% prediction interval (2012-03-02, 2015-12-22).
The first obvious thing about the expected update date and associated prediction interval is that the lower bound occurs before the release of the prior Mac Mini. This implies that a model with normal errors is unlikely to be appropriate. The second thing, possibly more obvious, is that the point estimate (expected update date) is over two years ago, furthermore only about three months after the last release date. The last release date being an extreme outlier. Ideally, these estimates should be revisited with an improved model.
The second model, for the expected delay, is more forgiving. The upper bound of the prediction interval is close to 3.5 years, giving us another 1.5 years or so to call the delay significant.
The Mac Mini did present a problem with an extended delay between the last and current iteration. The reason for this delay is unclear, making the identification of a good covariate such as Intel processor road maps problematic. The problem with the Intel road map covariate, is that there are CPUs available that fit the price and thermal requirements held by prior Mac Minis. These CPUs, available as of September 2015, include Intel Skylake i5 6260U, 6267U, and 6287U CPUs with the Intel i7 6567U for a high end SKU. Without a good covariate to help explain this change, the observations may indicate a change in release rate. If this is a change in release rate, it will be considerably more difficult to model the Mac Mini without moving to non-linear models.
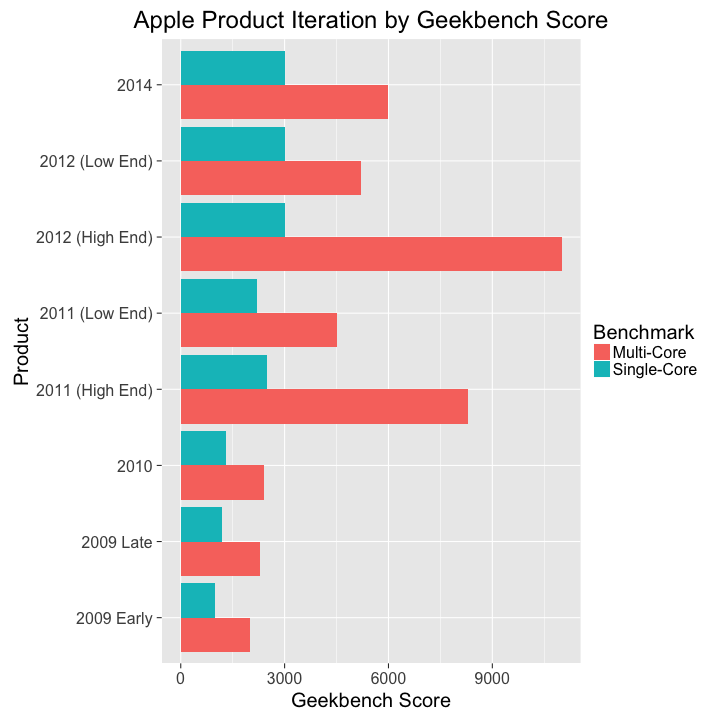
geekBench <- read.csv('geekbench.csv') library(ggplot2) theme_set(theme_gray(base_size = 20)) # plot product release dates by iteration p <- ggplot(geekBench, aes(x=Product,y=GeekbenchScore, fill=Benchmark)) + geom_bar(stat="identity",position="dodge") + coord_flip() + labs( title='Apple Product Iteration by Geekbench Score', y="Geekbench Score") plot(p)
There is also a chance that the model has been discontinued. Apple's Mac Mini advertisement page certainly doesn't help, where the mac mini is pictured next to a discontinued apple display.
Under the assumption that Apple likes to make a profit, we could use sales figures to get an idea if this product is likely to be discontinued (assuming that Apple isn't selling at a loss). Unfortunately, we don't have sales figures for the mac mini. Instead Amazon's Best Sellers could be used as at least a measure of popularity relative to other products. In this listing (as of 10:18AM EST on July 29, 2016) the mac mini holds place seven and eight with the 21.5" iMac showing up in ninth and the 27" iMac in twelfth. Although it is unclear what the window the sales are aggregated over ("Updated Hourly" doesn't necessarily imply single hour aggregation), the sales positions do imply someone is buying these.
For those interested, the eighth place product was the base model ($449) with a 1.4Ghz (2.7GHz Turbo Boost) CPU, 4GB of RAM and a 500GB hard drive. The seventh place Mac Mini ($649) had 8GB of RAM, a 2.6GHz (3.1GHz Turbo Boost) CPU and a 1TB hard drive.
This popularity is a bit surprising, given no real increase in single-core performance since 2011 and a decrease in multi-core performance since dropping the quad core model (Figure 8). However, the mac mini is only $449 at Amazon, a good $550 cheaper than the 21.5" iMac. This price and demand for some macOS based desktop computing seems to keep this product around, likely without much change in price or performance.
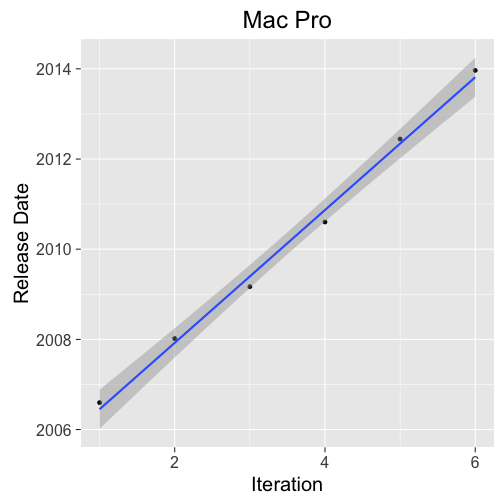
Mac Pro
Expected Update: 2015-04-15 with 95% prediction interval (2014-06-20, 2016-02-08).
The first model (Figure 9.) shows a fairly regular update cycle for the Mac Pro. Based on this regularity we would expect an update sometime around last month. This of course hasn't happened, as seen by my aging 2006 Mac Pro and my full piggy bank. This change in release date can't be adequately explained by lack of drop in CPU replacements, given that the 2011 pin Haswell and Broadwell chips have been skipped. Therefore, it is unclear if Apple is waiting for the next Intel chip or the second coming for a future update.
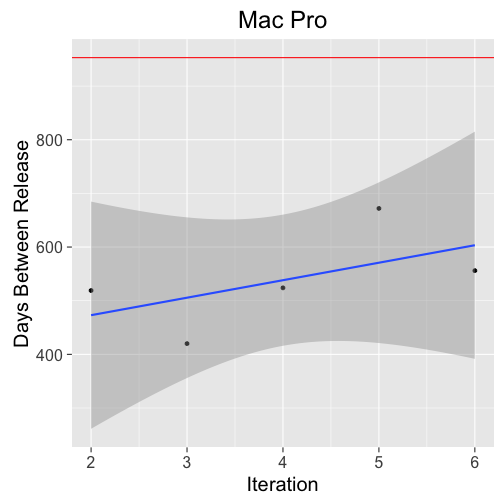
The second model (Figure 10.) agrees with the first with respect to the delay being significant. This model further shows an increase in the delay between releases; as mentioned earlier, there doesn't seem to be any obvious reason for this delay.
Like the Mac Mini, Apple doesn't provide breakouts for sales for just the Mac Pro so it is hard to determine if it was a flop or not. Even if it was a flop, there is always the argument for an aspiration product. But, it is not clear if this product is really aspiring, or if gazes have moved to more mobile devices.
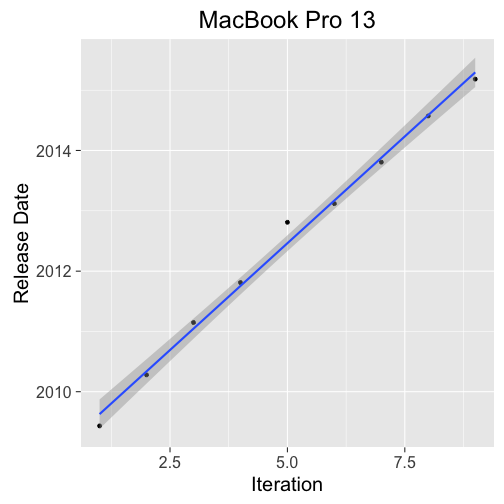
MacBook Pro 13"
Expected Update: 2016-01-02 with 95% prediction interval ( 2015-07-08, 2016-06-29).
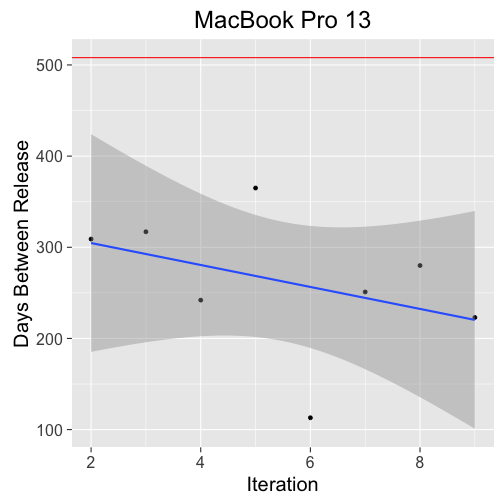
There isn't that much to say about the MacBook Pro 13", it's late. Furthermore, it's significantly late relative to other delays. Current rumors point to a release in Q4 2016, so the wait should come to an end soon.
The second model points to a decrease in delays, but the variability is sufficiently high to reverse directions after a few late releases.
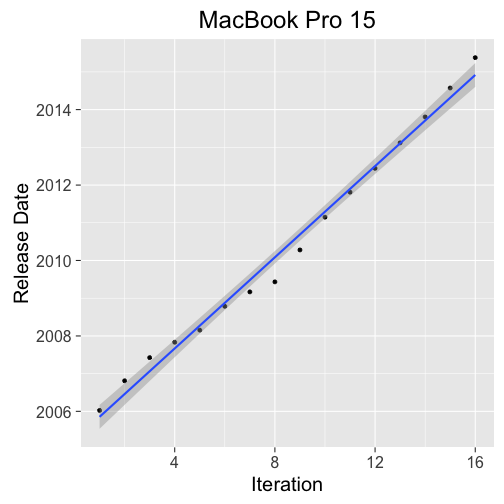
MacBook Pro 15"
Expected Update: 2015-07-11 with 95% prediction interval (2014-10-10, 2016-04-09).
Like the 13" model the 15" MacBook Pro is likely to get an update soon. Unlike the 13", the 15" model seemed to have slightly less variance, this seems to be at least in part due to the discrete GPU in the more recent models. If we take a look at the last update in the MacBook Pro line, it met it's release date not by upgrading the CPU but by only upgrading the GPU.